R1 1 Math I 1

グラフが図のようになる2次関数
\(y=ax^2+bx+c\)
を考える。

このとき、\(a,b,c\)は次の式を満たす。

\[\begin{align*} a < 0 \\ b > 0 \\ c > 0 \end{align*}\]

\(a\)は上に凸だから\(a<0\)となる。

\(b\)は\(y=ax^2+bx+c\)を平方完成した後の式と頂点座標は、

\[y=a(x+{b\over2a})^2+{-b^2+4ac\over4a}\]

\[(x,y)=({-b\over2a},{-b^2+4ac\over4a})\]

となる。
だから図のグラフの軸は\(x={-b\over2a}\)であり、図のグラフより\(x=0\)、Y軸線よりも右側にあることが分かる。つまり、

\[ \begin{align*} x={-b\over2a}>0 \\ {-b\over2a}>0 \\ \tag{$※a<0だから{-1\over2a}は正$} b>0 \end{align*} \]

である。

\(c\)は図のグラフより\(x=0\)の時、\(y>0\)と読み取れるから、

\[\begin{align*} y=a\cdot0^2+b\cdot0+c>0\\ y=c>0\\ c>0 \end{align*}\]

図のグラフより\((x,y)=(1,0)\)であるから、\(y=ax^2+bx+c\)に代入すると、

\[\begin{align*} 0=a\cdot1^2+b\cdot1+c\\ 0=a+b+c\\ a+b+c=0 \end{align*}\]

図のグラフより\(x=-1\)の時、\(y<0\)であるから、\(y=ax^2+bx+c\)に代入すると、

\[\begin{align*} 0>y=a\cdot(-1)^2+b\cdot(-1)+c\\ 0>y=a-b+c\\ y=a-b+c<0\\ a-b+c<0 \end{align*}\]

図のグラフより\(x=2\)の時、\(y<0\)であるから、\(y=ax^2+bx+c\)に代入すると、

\[\begin{align*} 0>y=a\cdot2^2+b\cdot2+c\\ 0>y=4a+2b+c\\ y=4a+2b+c<0\\ 4a-2b+c<0 \end{align*}\]

頂点座標\((x,y)=({-b\over2a},{-b^2+4ac\over4a})\)より、頂点yは0より大きいから、

\[\begin{align*} {-b^2+4ac\over4a}>0\\ \tag{※a<0}-b^2+4ac<0\\ b^2-4ac>0 \end{align*}\]

\(a,b,c\)が以下を満たす時、\(a^2-8b-8c\)が最小になる場合を考える。

\[\begin{align*} a < 0 \\ b > 0 \\ c > 0 \\ a+b+c=0 \end{align*}\]

この時、\(a+b+c=0\)より\(b+c=-a\)だから

\[\begin{align*} a^2-8b-8c&=a^2-8(b+c)\\ &=a^2-8(-a)\\ &=a^2+8a\\ &=(a+4)^2-16 \end{align*}\]

となるので、\(a=-4\)の時、\(a^2-8b-8c\)が最小になる。
\(y=ax^2+bx+c\)を\(b\)を用いて表すと

\[\begin{align*} a+b+c&=0\\ c&=-b-a\\ &=-b-(-4)\\ &=-b+4\\ \end{align*}\]

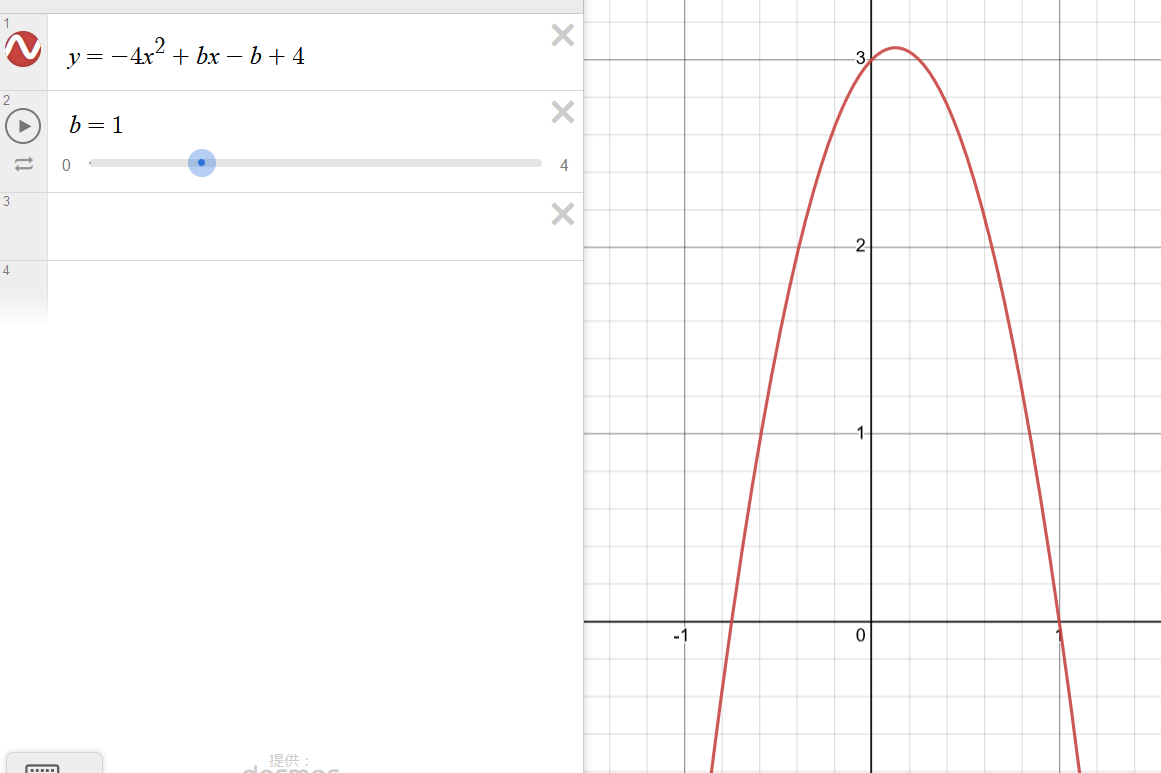
なので、\(y=-4x^2+bx-b+4\)となる。
また、\(b\)の値の範囲は元の式と\(b\)を用いて表した式を対応させると、

\[ \begin{align*} y&=ax^2+bx+c\\ y&=-4x^2+bx-b+4 \end{align*} \]

\[ \begin{align*} a&=-4\\ b&=b\\ c&=-b+4 \end{align*} \]

\(c>0\)であるから

\[ \begin{align*} c=-b+4>0\\ 4>b\\ b<4 \end{align*} \]

\( b \gt 0 \)と合わせると、\(b\)の範囲は\( 0 \lt b \lt 4 \)となる。